Continuando a sequência de posts sobre lógica sequencial, vamos falar hoje deste outro elemento da lógica sequencial: o flip-flop JK, que, a princípio, pode ser entendido como um flip-flop SR melhorado. Então, sem mais delongas, vamos ao post de hoje.
A imagem abaixo mostra o interior de um flip-flop JK com entrada de clock e é nesta imagem que iremos basear nosso estudo.
Basicamente é um flip-flop SR com uma realimentação um pouco diferente. A ideia é montarmos uma tabela igual à montada no post sobre o Flip-Flop SR, alguns posts atrás.
1) Se J=0 e K=0, vamos ver o que acontece:
* Se Q=0 e Q'=1: Neste caso a saída da porta AND de cima é 0 e da porta AND de baixo é 0 também.
Assim, as entradas R e S do Flip-Flop SR "interno" são 0 e as saídas continuam iguais ao do estado anterior. Ou seja, Q=0 e Q'=1.
* Se Q=1 e Q'=0: Neste caso a saída da porta AND de cima é 0 e da porta de baixo é também é 0. Com isso as entradas S e R do Flip-Flop SR "interno" são 0 e a saída, novamente, permanece inalterada, ou seja Q=1 e Q'=0.
2) Se J=1 e K=0, vamos ver o que acontece:
* Se Q=0 e Q'=1: Neste caso a saída da porta AND de cima é 1 e da porta AND de baixo é 0. Com isso a entrada S=1 e R=0 do Flip-Flop SR "interno". Assim a saída Q=1 e Q'=0.
* Se Q=1 e Q'=0: Neste caso a saída da porta AND de cima é 0, assim como a da porta de baixo. Com isso as entradas S e R do Flip-Flop SR "interno" são ambas 0 e as saídas continuam como estão, ou seja, Q=1 e Q'=0.
3) Se J=0 e K=1, vamos ver o que acontece:
* Se Q=0 e Q'=1: Neste caso a saída da porta AND de cima é 0, assim como a saída da porta AND de baixo. Com isso ambas as entradas do Flip-Flop SR "interno" são 0 e a saída se mantém do jeito que estava, ou seja, com Q=0 e Q'=1.
* Se Q=1 e Q'=0: Neste caso a saída da porta AND de cima é 0, porém a saída da porta AND de baixo é 1. Dessa forma, a entrada S é 0 e a entrada R é 1 do Flip-Flop SR "interno". Assim, a saída Q se torna 0 e Q' se torna 1. Com isso, acabamos por ter Q=0 e Q'=1.
Se você conhece o Flip-Flop SR, você talvez tenha percebido que o Flip-Flop JK, até agora, se comportou de forma igual ao Flip-Flop SR, sendo a entrada J similar a entrada S e a entrada K similar a entrada R. Então, qual a diferença do Flip-Flop JK para o Flip-Flop anterior, o SR? A resposta vem agora...
4) Se J=1 e K=1, vamos ver o que acontece:
* Se Q=0 e Q'=1: Neste caso a saída da porta AND de cima é 1 e a saída da porta AND de baixo é 0. Dessa forma a entrada S=1 e R=0 do Flip-Flop SR "interno". Com isso terminamos com Q=1 e Q'=0.
* Se Q=1 e Q'=0: Neste caso a saída da porta AND de cima é 0 e a saída da porta AND de baixo é 1. Dessa forma temos S=0 e R=1 no Flip-Flop SR "interno". Com isso terminamos com Q=0 e Q'=1.
Agora vemos a diferença entre os dois flip-flops. Enquanto o Flip-Flop SR não aceitava as duas entradas sendo 1 simultaneamente, o Flip-Flop JK aceita. Quando isso acontece, o Flip-Flop JK inverte o estado das saídas. Assim, se a saída Q era 1 passa a ser 0 e, se a saída Q era 0, passa a ser 1. Neste caso percebemos novamente a importância de um sinal de Clock. Caso não houvesse clock, se colocássemos 1 em ambas as entradas do Flip-Flop JK, a saída ficaria alternando rapidamente, pois não haveria um sinal para sincronizar a operação deste flip-flop.
E por hoje era isso. Nos vemos ano que vem, e que venha 2013. Abraço e continuem estudando. Qualquer dúvida, sugestão ou correção, usem os comentários. Fui!
Marcadores
- As crônicas de Peludu (4)
- Componentes (9)
- Computação (10)
- Conhecimentos Gerais (25)
- Dia-a-Dia (29)
- ENEM (8)
- Especial (21)
- Ferramentas da Qualidade (1)
- Físicas e Matemáticas (5)
- LaTeX (22)
- Pêndulo Invertido (3)
- Projetos (5)
- Questões Resolvidas (14)
- Resumo (2)
- Sobre Eletrônica (62)
- Softwares (1)
segunda-feira, 31 de dezembro de 2012
segunda-feira, 24 de dezembro de 2012
Fim de 2012
Enfim, o mundo não acabou, mas o ano está prestes a acabar. Fazendo um balanço desse ano, posso afirmar que foi um período bom, tanto para o blog quanto para minha vida pessoal e profissional.
Então desejo a todos que lêem este blog um feliz natal e um próspero ano novo, cheio de muita felicidade e conhecimento. Torço por um 2013 cheio de oportunidades para todos nós, e que possamos nos encontrar muitas vezes neste espaço.
Abraço e continuem estudando. Até 2013. \o/
Então desejo a todos que lêem este blog um feliz natal e um próspero ano novo, cheio de muita felicidade e conhecimento. Torço por um 2013 cheio de oportunidades para todos nós, e que possamos nos encontrar muitas vezes neste espaço.
Abraço e continuem estudando. Até 2013. \o/
sábado, 8 de dezembro de 2012
Iluminação Ep. 6: LED
Hoje eu declaro encerrado a série de iluminação falando de um último tópico importantíssimo. O LED, que provavelmente irá marcar o futuro da iluminação moderna. Vamos entender o que ele é então.
O LED é um dispositivo semicondutor que emite luz. Sua sigla significa Light Emitter Diode, ou seja, Diodo Emissor de Luz. Ele é realmente um diodo, que produz uma queda de tensão quando diretamente polarizado e a corrente que passa por ele nessa situação produz luz. O link abaixo possui explicações interessantes sobre o funcionamento físico e químico do LED e do processo de dopagem de material.
http://www.chemistry.wustl.edu/~edudev/LabTutorials/PeriodicProperties/MetalBonding/MetalBonding.html
Além disso há vários tipos de LED. Existem LED's bicolor, tricolor, infra-vermelho, ultra-violeta, RGB (que não deixa de ser tricolor também). Há também vários tamanhos, como 3mm, 5mm e 10mm, e também vários formatos, como redondo e retangular. Ou seja, a variedade de LEDs existente é enorme. Para os LEDs vale a seguinte regra: Pense em um LED. Ele provavelmente existe.
No começo de sua história, o LED foi usado exclusivamente para sinalização. Ele era usado em alguns equipamentos para mostrar o estado de seu funcionamento. Mas não era realmente levado a sério como tecnologia em iluminação pois ainda estava numa fase primitiva.
Com o passar do tempo foi começado a pensar na iluminação em LED com interesse comercial. Isso culminou em empresas que hoje investem nessa tecnologia em lâmpadas. Estima-se que até 2020 cerca de 90% de toda a iluminação seja feita com tecnologia LED. Então, vamos dar uma olhada nas características técnicas desse tipo de lâmpada.
* Eficiência Energética: Bastante Alta. A eficiência energética de um LED é sua grande vantagem. Lâmpadas de LED tem, facilmente, 80% de eficiência e uma nova tecnologia de LEDs, chamada de OLED (Organic LED) promete uma eficiência muito maior.
* Durabilidade: A duração de um LED pode chegar a até 100 mil horas, batendo facilmente a duração de Lâmpadas Incandescentes e Fluorescentes.
* Temperatura de Cor: A luz da lâmpada de LED é muito mais branca que da Lâmpada Incandescente, produzindo uma iluminação melhor.
* Custo: O custo do investimento incial ainda é alto. Mas com o passar do tempo, se o público realmente se interessar pela aquisição desses produtos, o preço com certeza cairá.
E para terminar, gostaria de mostrar a minha lâmpada de LED, que está na imagem abaixo. Eu a fiz no final do ano passado (2011) sob a orientação do meu professor e acabei apresentando-a na feira de tecnologia daquele ano.
Enclausurada na parte do soquete está uma fonte chaveada cuja saída possui 24V com capacidade para 500mA, entregando 12W para o conjunto de 140 LED's brancos de alto-brilho. A potência consumida pela lâmpada da rede elétrica não foi medido, mas não deve ultrapassar 15W, devido à alta eficiência da fonte chaveada. Outros cálculos, como fator de potência, também não foram efetuados na época da construção e eu tenho preguiça de calculá-los hoje. :)
A imagem abaixo mostra ela acesa. Pode-se perceber que ela não deixa nada a desejar no quesito de iluminação. A fonte chaveada foi construída usando alguns dos componentes de reatores de lâmpadas fluorescentes queimadas, o que é bom, devido a reciclagem de componentes que acabariam, provavelmente, não recebendo o destino correto.
Enfim, depois de meses terminei a série iluminação. Espero que tenha esclarecido muitas dúvidas. Caso alguém tenha alguma sugestão, crítica ou dúvida, por favor: deixe um comentário. Abraço, se cuidem e boas festas de fim de ano para todos.
domingo, 25 de novembro de 2012
Associação de Resistores - Exercícios Resolvidos I
Olá a todos. Um leitor do blog apontou que a explicação sobre associação de resistores estava incompleta. Portanto, resolvi fazer um post sobre exercícios resolvidos.
O livro do qual tirei os exercícios é um que tenho em casa, e foi o mesmo que usei no meu ensino médio. O livro se chama Universo da Física 3 - Ondulatória, Eletromagnetismo e Física Moderna, 2ª Edição, São Paulo, 2005. Os autores são José Luiz Sampaio e Caio Sérgio Calçada.
Sampaio é bacharel em física pelo Instituto de Física da Universidade de São Paulo e professor de física na rede particular de ensino desde 1968, enquanto Calçada é bacharel em matemática e engenheiro eletricista pela Escola Politécnica da Universidade de São Paulo e professor de física na rede particular de ensino desde 1968 também.
Este livro eu acho muito bom. Eu o adquiri para lê-lo por completo, sabendo que o plano curricular da minha escola não cobria todo o livro e digo, valeu a pena. Mas vamos direto ao ponto.
P. 73 Exercício 1) No circuito ao lado, a bateria e o amperímetro são ideais e os fios de ligação têm resistências desprezíveis. As lâmpadas têm resistências constantes, cujos valores são R1=2 Ohms e R2=3 Ohms e a força eletromotriz da bateria é E=12V.
a) Faça o diagrama correspondente a esse circuito.
b) Qual é a resistência equivalente das duas lâmpadas?
c) Qual é a marcação do amperímetro?
Acima está a resposta da letra A. No diagrama aparecem a bateria de 12V, os dois resistores em série de 2 e 3 Ohms respectivamente, e o amperímetro em série com o circuito, como deve ser.
A letra B solicita a resistência equivalente das lâmpadas. Por estarem em série, somaremos as resistências de ambas as lâmpadas. Assim, a resistência equivalente será 5 Ohms.
A letra C pede a marcação do amperímetro. Como o amperímetro é o instrumento que mede corrente, o exercício esta pedindo, de forma um pouco implícita, a corrente que está passando pelo amperímetro. Como o amperímetro está em série com os resistores, e a corrente por um circuito série é a mesma para todos os componentes que estão em série, o exercício pede a corrente que passa pelos resistores.
Descobrimos que a resistência equivalente dos dois resistores é 5 Ohms. Como no enunciado do exercício ele informa que o amperímetro é ideal, concluímos que sua resistência é nula e, portanto, não altera a resistência equivalente do circuito. Com isso temos uma tensão de 12V aplicada a uma resistência total de 5 Ohms. Então, a corrente no circuito é a divisão de 12 por 5 (Lei de Ohm) que resulta em 2,4A, que é a marcação que será indicada pelo amperímetro.
P. 121 Exercício 149) (PUC-SP) Numa experiência em São Paulo (tensão 110V) é utilizada a associação de resistores acima. Querendo utilizar a mesma montagem numa experiência realizada em Santos (tensão 220V), para que não haja alteração dos valores da corrente em cada resistor deve-se associar uma resistência R5:
a) de valor 8,4 Ohms em série com R1;
b) de valor 10 Ohms em série com R1;
c) de valor 8,4 Ohms em paralelo com R1;
d) de valor 10 Ohms em paralelo com R1;
e) de valor 1,6 Ohms em série com R1;
E é fácil ver que a resposta é a letra b.
Como cheguei neste valor. Da seguinte maneira:
O exercício pede que seja associado um resistor que mantenha as correntes no circuito iguais as que eram quando o circuito estava ligado em 110V. Se eu vou ligar em 220V, eu tenho que achar um resistor que, quando em série com o circuito, segure sobre ele metade da tensão, ou seja, 110V. Dessa forma continuará tendo 110V nos terminais do circuito e, dessa forma, as correntes se manterão iguais.
Vimos no exercício anterior que em série a tensão se divide. Como queremos dividir de forma igual a tensão de 220V temos que associar dois valores de resistências iguais. Assim, temos que achar a resistência equivalente do circuito mostrado na figura. Começamos pelos 3 resistores em paralelo:
![\frac{1}{R_{eq}}=\frac{1}{8}+\frac{1}{4}+\frac{1}{4}=\frac{1}{8}+\frac{2}{4}=\frac{1}{8}+\frac{1}{2} [;\frac{1}{R_{eq}}=\frac{1}{8}+\frac{1}{4}+\frac{1}{4}=\frac{1}{8}+\frac{2}{4}=\frac{1}{8}+\frac{1}{2};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_sq3mIuiNqSZgF-zdZCnciyMb8paGVGG7xG-L0s7w7x14c4JX0b1BK5gtnplQjIP28Wq1i-7oxfs8mRFMiVpngjs8zxuS7FJE_RXRJXiDvgqVGe29xN6EzKbyniluKzXlrqH7CS6yppXSuiAqXP_GFEY8UhYzae1ijSMWqThSZOH_c8bxpuOIUFhv2uSoSSVFOMKoOAlXcDgNgHxZ2g0aQX3wxpisFhL_EG3HAgOvDGhaDVYRwBFOdSVJagFt9fsEauNvzyWr7uuW43G0M0O607DXoI9-nOYiDqN7XZGoMtsaenGdJpGmrpkLiZpOljUW1nqSg_dkrL3w6k2hni-ppG03o=s0-d)
![\frac{1}{R_{eq}}=\frac{1}{8}+\frac{4}{8}=\frac{5}{8} [;\frac{1}{R_{eq}}=\frac{1}{8}+\frac{4}{8}=\frac{5}{8};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vEUW8dxyREw6oW9sxpsEu-iiBbfdJYW9iucHnUliu6WDI64uIvs7hpOyklME6XBC4iTcyM5BdMyZg8bxWePtbx-nHMuuR0XH9PiCY9gFhpmXYYo6TsZWbY3Ts3czcvYVcJ4dEzJcNY5ssEmrOqeuv3N9VJYq-j2bRl9utSvvfnviBIhtu1STolJNiuJ7H9_38AImxX3HKMBEWUqLOzOY2kCPxZGx6Jabk=s0-d)
Invertendo toda a equação:
![R_{eq}=\frac{8}{5}=1,6{\Omega} [;R_{eq}=\frac{8}{5}=1,6{\Omega};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_t7U_6CUmIwyTt6HRSs1H2cIKGEd4fCxgbDCNGcDFWdvH_PV-EhW5cxkzAMTImO11eqIMERJ1mSGUcKUxPN-_FLedk3cgDWeYyWuhrlz-_BBVpweF6FdyCBH1QSIjbTi3pRh2lwr2w5bJzGuqNMSbCWU_USfVUUvidt=s0-d)
Essa resistência equivalente, que saiu dos resistores em paralelo, está em série com aquele resistor de 8,4 Ohms na entrada do circuito. Desta forma somamos a resistência equivalente dos paralelos (1,6) com a resistência em série do circuito (8,4) e obtemos, como resistência equivalente de todo o circuito, 10 Ohms.
Então, uma resistência de quantos ohms devemos colocar em série para que metade dos 220V vá para o circuito e metade fique no resistor? Devemos associar um resistor em série com o circuito com o mesmo valor de sua resistência equivalente. Ou seja, um resistor de 10 Ohms em série resolve o problema. Portanto, assinale a letra B e esteja um pouco mais perto de estudar na PUC de São Paulo.
Vamos analisar por que as outras alternativas estão incorretas.
A letra A e E estão incorretas pois, se associarmos em série com o circuito resistores cujos valores não são iguais ao do circuito, não iremos dividir os 220V de forma igual entre o resistor e o circuito. Se não chegar ao circuito metade dos 220V, ou seja, exatamente 110V, os valores das correntes vão mudar e, portanto, o enunciado do exercício não será satisfeito.
Agora vamos analisar a letra C e D. Se associarmos qualquer coisa em paralelo com R1, a resistência equivalente no lugar de R1 será menor que os 8,4 Ohms. Por exemplo, se associarmos 8,4 Ohms em paralelo com R1 teremos 4,2 Ohms equivalentes e se associarmos 10 Ohms em paralelo com R1 teremos 4,56 Ohms equivalentes no lugar de R1. Dessa forma, além de termos todos os 220V entrando no circuito, teremos um resistor em série com o circuito menor, o que causará um aumento considerável de corrente em todos os resistores do circuito. Novamente, essas alternativas não atendem o enunciado do exercício.
E era isso, peguei um exercício fácil de associação série e um de associação misto, que permitiu vermos os conceitos de associação série e paralelo, além de divisão de corrente e tensão. Qualquer dúvida, sugestão ou apontamento de erros, deixe um comentário. Abraço e continuem estudando (principalmente quem for prestar vestibular!). Até mais...
O livro do qual tirei os exercícios é um que tenho em casa, e foi o mesmo que usei no meu ensino médio. O livro se chama Universo da Física 3 - Ondulatória, Eletromagnetismo e Física Moderna, 2ª Edição, São Paulo, 2005. Os autores são José Luiz Sampaio e Caio Sérgio Calçada.
Sampaio é bacharel em física pelo Instituto de Física da Universidade de São Paulo e professor de física na rede particular de ensino desde 1968, enquanto Calçada é bacharel em matemática e engenheiro eletricista pela Escola Politécnica da Universidade de São Paulo e professor de física na rede particular de ensino desde 1968 também.
Este livro eu acho muito bom. Eu o adquiri para lê-lo por completo, sabendo que o plano curricular da minha escola não cobria todo o livro e digo, valeu a pena. Mas vamos direto ao ponto.
P. 73 Exercício 1) No circuito ao lado, a bateria e o amperímetro são ideais e os fios de ligação têm resistências desprezíveis. As lâmpadas têm resistências constantes, cujos valores são R1=2 Ohms e R2=3 Ohms e a força eletromotriz da bateria é E=12V.
a) Faça o diagrama correspondente a esse circuito.
b) Qual é a resistência equivalente das duas lâmpadas?
c) Qual é a marcação do amperímetro?
Acima está a resposta da letra A. No diagrama aparecem a bateria de 12V, os dois resistores em série de 2 e 3 Ohms respectivamente, e o amperímetro em série com o circuito, como deve ser.
A letra B solicita a resistência equivalente das lâmpadas. Por estarem em série, somaremos as resistências de ambas as lâmpadas. Assim, a resistência equivalente será 5 Ohms.
A letra C pede a marcação do amperímetro. Como o amperímetro é o instrumento que mede corrente, o exercício esta pedindo, de forma um pouco implícita, a corrente que está passando pelo amperímetro. Como o amperímetro está em série com os resistores, e a corrente por um circuito série é a mesma para todos os componentes que estão em série, o exercício pede a corrente que passa pelos resistores.
Descobrimos que a resistência equivalente dos dois resistores é 5 Ohms. Como no enunciado do exercício ele informa que o amperímetro é ideal, concluímos que sua resistência é nula e, portanto, não altera a resistência equivalente do circuito. Com isso temos uma tensão de 12V aplicada a uma resistência total de 5 Ohms. Então, a corrente no circuito é a divisão de 12 por 5 (Lei de Ohm) que resulta em 2,4A, que é a marcação que será indicada pelo amperímetro.
P. 121 Exercício 149) (PUC-SP) Numa experiência em São Paulo (tensão 110V) é utilizada a associação de resistores acima. Querendo utilizar a mesma montagem numa experiência realizada em Santos (tensão 220V), para que não haja alteração dos valores da corrente em cada resistor deve-se associar uma resistência R5:
a) de valor 8,4 Ohms em série com R1;
b) de valor 10 Ohms em série com R1;
c) de valor 8,4 Ohms em paralelo com R1;
d) de valor 10 Ohms em paralelo com R1;
e) de valor 1,6 Ohms em série com R1;
E é fácil ver que a resposta é a letra b.
Como cheguei neste valor. Da seguinte maneira:
O exercício pede que seja associado um resistor que mantenha as correntes no circuito iguais as que eram quando o circuito estava ligado em 110V. Se eu vou ligar em 220V, eu tenho que achar um resistor que, quando em série com o circuito, segure sobre ele metade da tensão, ou seja, 110V. Dessa forma continuará tendo 110V nos terminais do circuito e, dessa forma, as correntes se manterão iguais.
Vimos no exercício anterior que em série a tensão se divide. Como queremos dividir de forma igual a tensão de 220V temos que associar dois valores de resistências iguais. Assim, temos que achar a resistência equivalente do circuito mostrado na figura. Começamos pelos 3 resistores em paralelo:
Invertendo toda a equação:
Essa resistência equivalente, que saiu dos resistores em paralelo, está em série com aquele resistor de 8,4 Ohms na entrada do circuito. Desta forma somamos a resistência equivalente dos paralelos (1,6) com a resistência em série do circuito (8,4) e obtemos, como resistência equivalente de todo o circuito, 10 Ohms.
Então, uma resistência de quantos ohms devemos colocar em série para que metade dos 220V vá para o circuito e metade fique no resistor? Devemos associar um resistor em série com o circuito com o mesmo valor de sua resistência equivalente. Ou seja, um resistor de 10 Ohms em série resolve o problema. Portanto, assinale a letra B e esteja um pouco mais perto de estudar na PUC de São Paulo.
Vamos analisar por que as outras alternativas estão incorretas.
A letra A e E estão incorretas pois, se associarmos em série com o circuito resistores cujos valores não são iguais ao do circuito, não iremos dividir os 220V de forma igual entre o resistor e o circuito. Se não chegar ao circuito metade dos 220V, ou seja, exatamente 110V, os valores das correntes vão mudar e, portanto, o enunciado do exercício não será satisfeito.
Agora vamos analisar a letra C e D. Se associarmos qualquer coisa em paralelo com R1, a resistência equivalente no lugar de R1 será menor que os 8,4 Ohms. Por exemplo, se associarmos 8,4 Ohms em paralelo com R1 teremos 4,2 Ohms equivalentes e se associarmos 10 Ohms em paralelo com R1 teremos 4,56 Ohms equivalentes no lugar de R1. Dessa forma, além de termos todos os 220V entrando no circuito, teremos um resistor em série com o circuito menor, o que causará um aumento considerável de corrente em todos os resistores do circuito. Novamente, essas alternativas não atendem o enunciado do exercício.
E era isso, peguei um exercício fácil de associação série e um de associação misto, que permitiu vermos os conceitos de associação série e paralelo, além de divisão de corrente e tensão. Qualquer dúvida, sugestão ou apontamento de erros, deixe um comentário. Abraço e continuem estudando (principalmente quem for prestar vestibular!). Até mais...
sexta-feira, 23 de novembro de 2012
Lógica Sequencial - Flip-Flop SR
Olá a todos. Hoje vamos falar um pouco sobre lógica sequencial. É interessante, para este post, ter o conhecimento sobre lógica combinacional e portas lógicas, que pode ser encontrado no post "Lógica Combinacional - Portas Lógicas", ou no livro Elementos de Eletrônica Digital, de Idoeta e Capuano.
Bom, vamos começar definindo o que é lógica sequencial. Para tanto, vamos dar uma rápida revisada na definição de lógica combinacional.
Um circuito digital combinacional é aquele cuja saída depende única e exclusivamente das entradas em um dado momento. Porém, na lógica sequencial a saída agora depende das entradas de agora e de como a saída estava antes.
Essa definição até que é boa, mas temos que trabalhar um pouco nela e definir o quão antes. Pois dizer que a saída de agora depende da saída de antes não informa se era a saída de 1 segundo atrás ou o estado da saída ontem!
Para resolver esse "problema" os sistemas digitais sequenciais trabalham respeitando um sinal de clock. Você com certeza já ouviu falar neste termo, pelo menos implicitamente. Quando falamos que um processador de PC trabalha com 3GHz, estamos falando justamente deste tal de clock. Ele, dessa forma, acaba definindo a velocidade com o que o sistema digital trabalha.
Para nossos exemplos, vamos considerar um sinal de clock de 1Hz, o que dá um período de 1 segundo. Isto significa que cada transição, cada mudança de estado vai acontecer a cada 1 segundo. Dessa forma, podemos usar aquela definição de lógica combinacional e dizer que o estado da saída agora depende das entradas agora e de como estava a saída 1 segundo atrás.
Parando para pensar (ou você também pode pensar caminhando, como preferir), se nós dizemos que a saída agora depende do estado de antes, isto significa que em lógica sequencial nós trabalhamos com a ideia de memória. Nós conseguimos (e com "nós", me refiro ao sistema digital...) lembrar o estado de antes para definir o estado atual. Para estudar este fenômeno novo, vamos trabalhar com o elemento mais simples da lógica sequencial. Se em combinacional o elemento mais simples era uma porta lógica, agora em sequencial o elemento mais simples será o flip-flop SR (ou RS).
Vamos explicar algumas coisas para analisar este circuito. Ele possui duas entradas, que se chamam S (Set) e R (Reset) e duas saídas que são Q e Q'. A saída Q' é simplesmente Q negado (Q negativo). Ou seja, se Q for 1, Q' obrigatoriamente deverá ser 0 e vice-versa.
Vamos começar supondo R=0 e S=0. Se a saída anterior era Q=0, então Q'=1. Dessa forma na porta NOR de cima temos R e Q' (0 nor 1) como entradas que resulta em Q=0. Na porta NOR de baixo temos S e Q (0 nor 0) como entradas que resultam em Q'=1 como saída.
Supondo as mesmas entradas ainda, R=0 e S=0, mas as saídas ao contrário, ou seja, Q=1 e Q'=0, teríamos na porta NOR de cima como entrada (0 nor 0) que resulta em Q=1 e na porta NOR de baixo teríamos como entrada (0 nor 1) que resultaria em Q'=0.
Vimos que se tanto R como S forem 0, a saída continua exatamente como está. Interpretamos isso da seguinte forma: se eu não estou Setando nem Resetando, então não estou fazendo nada. Se não faço nada, as coisas continuam iguais a como estavam antes.
Supondo R=1 e S=0, começando com Q=1 e Q'=0. Neste caso na porta NOR de cima a entrada seria (1 nor 0) que resulta em Q=0 e a porta NOR de baixo teria como entrada (0 nor 0), que resulta em Q'=1.
Supondo R=1 e S=0, mas dessa vez com Q=0 e Q'=1. Neste caso a porta NOR de cima tem como entrada (1 nor 1), apresentando como saída Q=0 e a NOR de baixo teria (0 nor 0) como entrada, apresentando Q'=1 como saída.
Ou seja, se eu tiver um sinal em R (Reset), eu obrigo a saída Q a ser igual a 0, ou seja, eu reseto o valor de Q. Fazendo Q valer zero eu, consequentemente, transformo Q' em 1. Se a saída Q já era 0 antes de eu ativar o RESET, a saída continua no estado 0.
Supondo dessa vez R=0 e S=1, com Q=1 e Q'=0. Temos então (0 nor 0) na NOR de cima, resultando em Q=1 e (1 nor 1) na NOR de baixo, resultando em Q'=0.
Supondo ainda R=0 e S=1, mas com Q=0 e Q'=1 dessa vez. Temos então (0 nor 1) na NOR de cima, resultando em Q=0 e (1 nor 0) na NOR de baixo, resultando em Q'=0.
De forma análoga ao caso do Reset, se eu tiver um sinal em S (Set), eu obrigo a saída Q a ser igual a 1, ou seja, eu Seto o valor de Q. Com isso eu obrigo, por consequência, a saída Q' a ser igual a 0. Se a saída Q já era 1 antes de eu ativar o SET, ela simplesmente continua valendo 1.
Últimos dois casos. Suponha R=1 e S=1, com Q=1 e Q'=0. Assim na NOR de cima temos (1 nor 0) resultando em Q=0 enquanto a NOR de baixo apresenta como entrada (1 nor 1) que dá como resultado Q'=0.
Por fim, suponha R=1 e S=1, agora com Q=0 e Q'=1. Na NOR de cima temos como entrada (1 nor 1) que resulta em Q=0 e na NOR de baixo temos (1 nor 0) que também resulta em Q'=0.
Perceba que se tanto R quanto S forem 1, temos que tanto Q quanto Q' são 0. Isso é um problema, pois definimos que Q' devia ser o contrário de Q. E imagine que tanto Q quanto Q' são 0. Agora eu faço tanto R quanto S valerem 0 também. Dessa forma a saída continua igual. Certo? Errado. Se R e S são 0 quando Q e Q' também são 0, então Q e Q' passam a valer ambos 1. Isso desfaz nossa definição que quando eu não estou setando nem resetando a saída permanece inalterada.
Por causa desses problemas, nenhum sistema sequencial que emprega flip-flop SR utiliza a última situação, como é mostrado pela nossa tabela verdade. Dizemos então que estas não são entradas válidas para o flip-flop SR e que devemos evitá-las.
Mas este flip-flop não está sendo influenciada por nenhum sinal de clock. Dessa forma o flip-flop não está funcionando de forma sincronizada e podemos colocar qualquer entrada qualquer hora que a saída irá mudar (a menos, claro, que ambas as entradas sejam zero). Essa situação de poder alterar a saída a qualquer hora é muito indesejável em algumas aplicações (como um computador, por exemplo). Então nossa missão agora é fazer o flip-flop funcionar (ou seja, permitir que sua saída mude de estado) somente em intervalos sincronizados e muito curtos. Dessa forma, solucionamos o problema com o seguinte circuito:
Abaixo está a imagem de um flip-flop com entrada para clock.
Esse flip-flop é similar ao anterior, mas com uma diferença. Ele só funciona quando o clock=1. Pois se clock for igual a 0, a saída da porta E vai ser zero independente dos valores de R e S e, dessa forma, a saída se manterá igual independente das entradas R e S. O flip-flop só vai ler mesmo as entradas R e S quando o sinal de clock for igual a 1.
Supondo que o clock dê um pulso de nível alto muito curto uma vez a cada 1 segundo. Dessa forma as saídas só vão ser atualizadas conforme as entradas do flip-flop a cada 1 segundo. Porém é importante que o pulso do clock seja muito breve. Pois se o pulso de clock for longo, é possível que o flip-flop leia duas entradas diferentes enquanto o clock estiver ativado e, assim, troque o estado da saída 2 vezes, o que é indesejável.
Existem, até onde eu sei, 4 tipos de "leitura" de clock. Um clock que é ativo com o sinal alto e um clock ativo com o sinal baixo. Esses dois tipos são ruins pois, em geral, o sinal de clock passa muito tempo em estado alto e baixo (considere como clock, por exemplo, um sinal com duty cicle igual a 50%). Com isso temos o problema de ser possível colocar duas entradas no mesmo pulso de clock, o que é indesejável.
Então é mais comum os outros dois tipos de clock, que são clocks por transição. Assim o clock fica ativo quando o clock passa do estado baixo para o alto ou do estado alto para o baixo. Com isso, o clock fica ativo por um tempo muito menor. Assim é muito mais difícil que o flip-flop receba duas entradas durante o tempo de clock ativo, pois o tempo de clock ativo é muito menor.
Com este post espero que tenham entendido a ideia de clock e a ideia de flip-flop SR. Recapitulando brevemente, clock é o pulso que faz todo o sistema digital funcionar de forma síncrona. Ele é como o maestro da grande orquestra da eletrônica digital. O flip-flop SR, que foi estudado neste post, é o elemento mais simples da eletrônica digital sequencial e o primeiro elemento que estudamos que contém a propriedade de memória, ou seja, ele se lembra de seu estado passado e usa essa informação para determinar o estado atual. Se o leitor que não conhecia flip-flops nem clocks sair deste post com essas informações bem compreendidas, já me considero um blogueiro feliz. *-*
E por hoje era isso. Ainda temos outros tipos de flip-flops para aprender (como um tipo que resolve o problema das duas entradas valendo 1) e, no futuro, veremos circuitos práticos com flip-flops (como um clapper simples, que aciona uma carga quando bate-se palmas!) que são muito interessentes. Então, até lá e se cuidem. E lembrem-se, qualquer dúvida, sugestão ou apontamento de erros no post, usem os comentários que eu costumo responder dentro de 1 dia.
Feedback people, please...
Bom, vamos começar definindo o que é lógica sequencial. Para tanto, vamos dar uma rápida revisada na definição de lógica combinacional.
Um circuito digital combinacional é aquele cuja saída depende única e exclusivamente das entradas em um dado momento. Porém, na lógica sequencial a saída agora depende das entradas de agora e de como a saída estava antes.
Essa definição até que é boa, mas temos que trabalhar um pouco nela e definir o quão antes. Pois dizer que a saída de agora depende da saída de antes não informa se era a saída de 1 segundo atrás ou o estado da saída ontem!
Para resolver esse "problema" os sistemas digitais sequenciais trabalham respeitando um sinal de clock. Você com certeza já ouviu falar neste termo, pelo menos implicitamente. Quando falamos que um processador de PC trabalha com 3GHz, estamos falando justamente deste tal de clock. Ele, dessa forma, acaba definindo a velocidade com o que o sistema digital trabalha.
Para nossos exemplos, vamos considerar um sinal de clock de 1Hz, o que dá um período de 1 segundo. Isto significa que cada transição, cada mudança de estado vai acontecer a cada 1 segundo. Dessa forma, podemos usar aquela definição de lógica combinacional e dizer que o estado da saída agora depende das entradas agora e de como estava a saída 1 segundo atrás.
Parando para pensar (ou você também pode pensar caminhando, como preferir), se nós dizemos que a saída agora depende do estado de antes, isto significa que em lógica sequencial nós trabalhamos com a ideia de memória. Nós conseguimos (e com "nós", me refiro ao sistema digital...) lembrar o estado de antes para definir o estado atual. Para estudar este fenômeno novo, vamos trabalhar com o elemento mais simples da lógica sequencial. Se em combinacional o elemento mais simples era uma porta lógica, agora em sequencial o elemento mais simples será o flip-flop SR (ou RS).
Análise da Tabela Verdade do Flip-Flop SR
Vamos explicar algumas coisas para analisar este circuito. Ele possui duas entradas, que se chamam S (Set) e R (Reset) e duas saídas que são Q e Q'. A saída Q' é simplesmente Q negado (Q negativo). Ou seja, se Q for 1, Q' obrigatoriamente deverá ser 0 e vice-versa.
Vamos começar supondo R=0 e S=0. Se a saída anterior era Q=0, então Q'=1. Dessa forma na porta NOR de cima temos R e Q' (0 nor 1) como entradas que resulta em Q=0. Na porta NOR de baixo temos S e Q (0 nor 0) como entradas que resultam em Q'=1 como saída.
Supondo as mesmas entradas ainda, R=0 e S=0, mas as saídas ao contrário, ou seja, Q=1 e Q'=0, teríamos na porta NOR de cima como entrada (0 nor 0) que resulta em Q=1 e na porta NOR de baixo teríamos como entrada (0 nor 1) que resultaria em Q'=0.
Vimos que se tanto R como S forem 0, a saída continua exatamente como está. Interpretamos isso da seguinte forma: se eu não estou Setando nem Resetando, então não estou fazendo nada. Se não faço nada, as coisas continuam iguais a como estavam antes.
Supondo R=1 e S=0, começando com Q=1 e Q'=0. Neste caso na porta NOR de cima a entrada seria (1 nor 0) que resulta em Q=0 e a porta NOR de baixo teria como entrada (0 nor 0), que resulta em Q'=1.
Supondo R=1 e S=0, mas dessa vez com Q=0 e Q'=1. Neste caso a porta NOR de cima tem como entrada (1 nor 1), apresentando como saída Q=0 e a NOR de baixo teria (0 nor 0) como entrada, apresentando Q'=1 como saída.
Ou seja, se eu tiver um sinal em R (Reset), eu obrigo a saída Q a ser igual a 0, ou seja, eu reseto o valor de Q. Fazendo Q valer zero eu, consequentemente, transformo Q' em 1. Se a saída Q já era 0 antes de eu ativar o RESET, a saída continua no estado 0.
Supondo dessa vez R=0 e S=1, com Q=1 e Q'=0. Temos então (0 nor 0) na NOR de cima, resultando em Q=1 e (1 nor 1) na NOR de baixo, resultando em Q'=0.
Supondo ainda R=0 e S=1, mas com Q=0 e Q'=1 dessa vez. Temos então (0 nor 1) na NOR de cima, resultando em Q=0 e (1 nor 0) na NOR de baixo, resultando em Q'=0.
De forma análoga ao caso do Reset, se eu tiver um sinal em S (Set), eu obrigo a saída Q a ser igual a 1, ou seja, eu Seto o valor de Q. Com isso eu obrigo, por consequência, a saída Q' a ser igual a 0. Se a saída Q já era 1 antes de eu ativar o SET, ela simplesmente continua valendo 1.
Últimos dois casos. Suponha R=1 e S=1, com Q=1 e Q'=0. Assim na NOR de cima temos (1 nor 0) resultando em Q=0 enquanto a NOR de baixo apresenta como entrada (1 nor 1) que dá como resultado Q'=0.
Por fim, suponha R=1 e S=1, agora com Q=0 e Q'=1. Na NOR de cima temos como entrada (1 nor 1) que resulta em Q=0 e na NOR de baixo temos (1 nor 0) que também resulta em Q'=0.
Perceba que se tanto R quanto S forem 1, temos que tanto Q quanto Q' são 0. Isso é um problema, pois definimos que Q' devia ser o contrário de Q. E imagine que tanto Q quanto Q' são 0. Agora eu faço tanto R quanto S valerem 0 também. Dessa forma a saída continua igual. Certo? Errado. Se R e S são 0 quando Q e Q' também são 0, então Q e Q' passam a valer ambos 1. Isso desfaz nossa definição que quando eu não estou setando nem resetando a saída permanece inalterada.
Por causa desses problemas, nenhum sistema sequencial que emprega flip-flop SR utiliza a última situação, como é mostrado pela nossa tabela verdade. Dizemos então que estas não são entradas válidas para o flip-flop SR e que devemos evitá-las.
Mas este flip-flop não está sendo influenciada por nenhum sinal de clock. Dessa forma o flip-flop não está funcionando de forma sincronizada e podemos colocar qualquer entrada qualquer hora que a saída irá mudar (a menos, claro, que ambas as entradas sejam zero). Essa situação de poder alterar a saída a qualquer hora é muito indesejável em algumas aplicações (como um computador, por exemplo). Então nossa missão agora é fazer o flip-flop funcionar (ou seja, permitir que sua saída mude de estado) somente em intervalos sincronizados e muito curtos. Dessa forma, solucionamos o problema com o seguinte circuito:
Abaixo está a imagem de um flip-flop com entrada para clock.
Esse flip-flop é similar ao anterior, mas com uma diferença. Ele só funciona quando o clock=1. Pois se clock for igual a 0, a saída da porta E vai ser zero independente dos valores de R e S e, dessa forma, a saída se manterá igual independente das entradas R e S. O flip-flop só vai ler mesmo as entradas R e S quando o sinal de clock for igual a 1.
Supondo que o clock dê um pulso de nível alto muito curto uma vez a cada 1 segundo. Dessa forma as saídas só vão ser atualizadas conforme as entradas do flip-flop a cada 1 segundo. Porém é importante que o pulso do clock seja muito breve. Pois se o pulso de clock for longo, é possível que o flip-flop leia duas entradas diferentes enquanto o clock estiver ativado e, assim, troque o estado da saída 2 vezes, o que é indesejável.
Existem, até onde eu sei, 4 tipos de "leitura" de clock. Um clock que é ativo com o sinal alto e um clock ativo com o sinal baixo. Esses dois tipos são ruins pois, em geral, o sinal de clock passa muito tempo em estado alto e baixo (considere como clock, por exemplo, um sinal com duty cicle igual a 50%). Com isso temos o problema de ser possível colocar duas entradas no mesmo pulso de clock, o que é indesejável.
Então é mais comum os outros dois tipos de clock, que são clocks por transição. Assim o clock fica ativo quando o clock passa do estado baixo para o alto ou do estado alto para o baixo. Com isso, o clock fica ativo por um tempo muito menor. Assim é muito mais difícil que o flip-flop receba duas entradas durante o tempo de clock ativo, pois o tempo de clock ativo é muito menor.
Com este post espero que tenham entendido a ideia de clock e a ideia de flip-flop SR. Recapitulando brevemente, clock é o pulso que faz todo o sistema digital funcionar de forma síncrona. Ele é como o maestro da grande orquestra da eletrônica digital. O flip-flop SR, que foi estudado neste post, é o elemento mais simples da eletrônica digital sequencial e o primeiro elemento que estudamos que contém a propriedade de memória, ou seja, ele se lembra de seu estado passado e usa essa informação para determinar o estado atual. Se o leitor que não conhecia flip-flops nem clocks sair deste post com essas informações bem compreendidas, já me considero um blogueiro feliz. *-*
E por hoje era isso. Ainda temos outros tipos de flip-flops para aprender (como um tipo que resolve o problema das duas entradas valendo 1) e, no futuro, veremos circuitos práticos com flip-flops (como um clapper simples, que aciona uma carga quando bate-se palmas!) que são muito interessentes. Então, até lá e se cuidem. E lembrem-se, qualquer dúvida, sugestão ou apontamento de erros no post, usem os comentários que eu costumo responder dentro de 1 dia.
Feedback people, please...
sábado, 27 de outubro de 2012
Baixa Frequência de Postagens
Agora que estamos no final do ano, estou cheio de trabalhos da universidade, do SENAI e do meu estágio. Devido a isso, a frequência de postagens baixou bastante. Mas garanto pra vocês que em dezembro voltaremos com força total. Até lá, peço paciência. E aviso que voltarei com postagens bem interessantes. Agradeço a todos pela compreensão e aguardem...
sexta-feira, 12 de outubro de 2012
Resumo da Série Conversores Chaveados
Aqui está um resumão da série de conversores chaveados operando no modo de condução contínua. Aqui está todos os posts dessa série e caso sejam feitos mais posts sobre o assunto, seus links serão anexados aqui.
Constam nessa série, até agora, os seguintes posts:
* Conversor Buck no Modo Contínuo
* Conversor Boost no Modo Contínuo
* Conversor Buck-Boost no Modo Contínuo
* Conversor Cuk no Modo Contínuo
* Conversor SEPIC no Modo Contínuo
A bibliografia usada nesta série foi o livro de Daniel W. Hart, eletrônica de potência: análise e projeto de circuitos. Na minha opinião, embora não tenha muita condição para comparar, acho um livro excelente e recomendo a todos que querem começar a aprender eletrônica de potência. As imagens foram retiradas, na maioria, do site Wikipedia.
Atualizado pela última vez em: 01/03/2014.
Constam nessa série, até agora, os seguintes posts:
* Conversor Buck no Modo Contínuo
* Conversor Boost no Modo Contínuo
* Conversor Buck-Boost no Modo Contínuo
* Conversor Cuk no Modo Contínuo
* Conversor SEPIC no Modo Contínuo
A bibliografia usada nesta série foi o livro de Daniel W. Hart, eletrônica de potência: análise e projeto de circuitos. Na minha opinião, embora não tenha muita condição para comparar, acho um livro excelente e recomendo a todos que querem começar a aprender eletrônica de potência. As imagens foram retiradas, na maioria, do site Wikipedia.
Atualizado pela última vez em: 01/03/2014.
Conversor SEPIC no Modo Contínuo
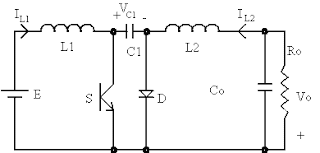
Olá a todos. Hoje vou falar sobre o conversor SEPIC (Single-Ended Primary Inductor Conversor), conversor com indutância simples no primário. É um conversor semelhante ao Cuk, no sentido em que pode rebaixar ou aumentar a tensão, mas sem o inconveniente de inversão de polaridade na saída. Abaixo está a imagem de seu circuito.
Vamos, como sempre, fazer algumas suposições para nossa análise.
1. Os valores dos indutores são muito altos e suas correntes são constantes.
2. Os valores dos capacitores são muito altos e suas tensões são constantes.
3. O circuito está funcionando no modo estável, ou seja, as formas de onda de tensão e corrente são periódicas.
4. Para uma taxa de trabalho D, a chave fica fechada por um tempo DT e aberta por um tempo (1-D)T.
5. Todos os componentes são ideais.
Vamos começar usando a Lei de Kirchoff das tensões na malha que contém a tensão de entrada, L1, Cs e L2. Assim, obtemos que:
![-V_{in}+v_{L1}+v_{Cs}-v_{L2}=0 [;-V_{in}+v_{L1}+v_{Cs}-v_{L2}=0;]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vqKAbFEfT7Z6PxBcYJK5yNCuoBCe6RAuzPRXEeutocorC-BBLjRtw5t9P9PQ4MPdKODBJr1MEbDa847FyG280XkaRzYQRVmfgrbOZyAtsl65bALKQyxE-25dqOvjtCgEhFOOUofkIw8bie5SOaJnGy_xcl=s0-d)
Lembrando que a tensão média nos indutores é igual a zero, podemos usar as tensões médias para obter:
![V_{Cs}=V_{in} [;V_{Cs}=V_{in};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_v4V4Cc3Ui4-IlT3S3Pae83C3-K5It1JzSspfU8Poc5ow57vPCiRzLMqR1DMEllV274GTOpJZF03QPlWa-ItjX5FoIpYHi6OSiFJSUn9Ii-ythIwW3zwOy6aQ=s0-d)
Quando a chave está fechada, o diodo está em corte e a tensão para L1 é igual a Vin. Quando a chave está aberta, o diodo entra em condução. Aplicando a lei das malhas de Kirchoff na malha mais externa, temos:
![-V_{in}+v_{L1}+v_{Cs}+V_{out}=0 [;-V_{in}+v_{L1}+v_{Cs}+V_{out}=0;]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_ujCbU2vKYqeprJog_DzGAxpyuVHNbVaQPWvxjnzmzomSQnezJGkFx_1QzO2zpg8r_SyeQkBU4phzqtAjmJJy4N3Vkp7BOsnuFXtVhrNZGq3ssTWxd6X_KsqSbh9qVX-nXkyzYiXK5DARFJJsdvCgNsTxALGg=s0-d)
Mas como a tensão média no capacitor Cs é igual a Vin, podemos escrever a expressão anterior como:
![v_{L1}=-V_{out} [;v_{L1}=-V_{out};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_sefzsQ-TjbcvsW7Y0J8vnyuBxopyj6C5LKW66p41llPY-wxvQdn5co1XbEZJMEPLBWcUNlM1YZ8wzN_MMIXQ68QuCxOYqo3nZZWreu7HXuaWV9_E4pB-GD0PcG2g=s0-d)
Sabemos que durante o tempo em que a chave está fechada a tensão em L1 é igual a Vin e durante o perído em que a chave está aberta a tensão em L1 é igual a -Vout. Também sabemos que durante um período a tensão média em um indutor é zero. Dessa forma, podemos escrever que:
![V_{in}.(DT)-V_{out}(1-D)T=0 [;V_{in}.(DT)-V_{out}(1-D)T=0;]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_sQo1FZIk6l7BLRXonOURCU6RUfdAs4Tbes9XOf8Pzd2SGgPB3ZodTqcIARbDrGBC5s57kZnQaqI0QtwTqPJZcEgFPTD9BkJcTOcBMRYoc5vecBxlhPl-CCMJf3fs5IBELlP1q9BWaWCQ=s0-d)
Assim temos que:
![V_{out}=V_{in}.\frac{D}{(1-D)} [;V_{out}=V_{in}.\frac{D}{(1-D)};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_uxPWSjP_lL8dT_Em6pi1Mt09xn6DNfXvDCzTgQA7mRDEGs1HkUt1qoLTnrprpkgYWSTgoDrYp5o5-MSdnODL4dQ5nhLhdo0vuW7LM-fbY0UZJOYuvzOhAlXzIFK-z-hJU5Z2oQS42nLuXXy6DDDbJE0iMRdA=s0-d)
Perceba que neste conversor a tensão de saída NÃO está invertida com relação a tensão de entrada. Também perceba a semelhança entre esta equação e as equações dos conversores Cuk e Buck-Boost.
E com isso encerramos nossa série sobre conversores. O que não significa que não iremos mais falar deles. Ainda existem muitas informações sobre conversores, como conversores intercalados, perdas de chaveamento, influência de ESR nos capacitores do conversor, etc. Mas isso ficará para outro momento. Espero que tenham gostado e entendido um pouquinho mais sobre conversores chaveados e suas utilidades. Um grande abraço e até a próxima.
Vamos, como sempre, fazer algumas suposições para nossa análise.
1. Os valores dos indutores são muito altos e suas correntes são constantes.
2. Os valores dos capacitores são muito altos e suas tensões são constantes.
3. O circuito está funcionando no modo estável, ou seja, as formas de onda de tensão e corrente são periódicas.
4. Para uma taxa de trabalho D, a chave fica fechada por um tempo DT e aberta por um tempo (1-D)T.
5. Todos os componentes são ideais.
Vamos começar usando a Lei de Kirchoff das tensões na malha que contém a tensão de entrada, L1, Cs e L2. Assim, obtemos que:
Lembrando que a tensão média nos indutores é igual a zero, podemos usar as tensões médias para obter:
Quando a chave está fechada, o diodo está em corte e a tensão para L1 é igual a Vin. Quando a chave está aberta, o diodo entra em condução. Aplicando a lei das malhas de Kirchoff na malha mais externa, temos:
Mas como a tensão média no capacitor Cs é igual a Vin, podemos escrever a expressão anterior como:
Sabemos que durante o tempo em que a chave está fechada a tensão em L1 é igual a Vin e durante o perído em que a chave está aberta a tensão em L1 é igual a -Vout. Também sabemos que durante um período a tensão média em um indutor é zero. Dessa forma, podemos escrever que:
Assim temos que:
Perceba que neste conversor a tensão de saída NÃO está invertida com relação a tensão de entrada. Também perceba a semelhança entre esta equação e as equações dos conversores Cuk e Buck-Boost.
E com isso encerramos nossa série sobre conversores. O que não significa que não iremos mais falar deles. Ainda existem muitas informações sobre conversores, como conversores intercalados, perdas de chaveamento, influência de ESR nos capacitores do conversor, etc. Mas isso ficará para outro momento. Espero que tenham gostado e entendido um pouquinho mais sobre conversores chaveados e suas utilidades. Um grande abraço e até a próxima.
sexta-feira, 21 de setembro de 2012
Conversor Cuk no Modo Contínuo
Olá a todos, hoje falaremos de uma topologia de conversor chaveado CC-CC chamada Conversor Cuk. Ele serve para elevar ou rebaixar a tensão de entrada e, assim como o conversor Buck-Boost, e também possui a polaridade de saída invertida com relação a entrada. Sua principal diferença é o fato de que esta topologia usa um capacitor para fazer a transferência de energia entre os dois estágios, diferente do conversor Buck-Boost que utiliza um indutor.
Segue abaixo uma imagem do conversor Cuk:
Para analisarmos este conversor, determinaremos, assim como fizemos com os outros, algumas condições que facilitam os cálculos e garantem o funcionamento no modo contínuo e no estado estável.
1. Os valores de indutores são altos e suas correntes são constantes;
2. Os valores dos capacitores são altos e suas tensões constantes;
3. As formas de onda de tensão e corrente são periódicas;
4. A chave (no caso o transistor) fica fechado durante um tempo DT e aberto durante um tempo (1-D)T onde D é a taxa de trabalho e T é o período;
5. Todos os componentes são ideais.
Descobriremos a tensão média no capacitor utilizando a Lei de Kirchhoff na malha externa. Sabendo que durante um período a tensão média nos indutores é zero, calculamos que a tensão média no capacitor durante um período de trabalho é a tensão de entrada menos a tensão de saída, ou seja:
![V_{c1}=V_E-V_o [;V_{c1}=V_E-V_o;]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_u2JeMJnSPgMiJfkvWdeZTGpLRxY8tgWofFvycO3_UdKm-Qq4gdrNE2ZsfbU0Y2DY3bAQWLyQo9-pNw8O3hbhmTwH7E3-IUx0ZcPKVRnLqK3TsfuGJo58s=s0-d)
Com a chave fechada, o diodo estará reversamente polarizado. Dessa forma, a corrente no capacitor C1 será:
![I_{c1}=-I_{L2} [;I_{c1}=-I_{L2};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_soLLLjuHXhZfledbDf_mHmfhhXmbCPTac55NQSsAEr1ZSgkZ8pmj1SZe5ALNrhlsfpjMkP4JseTZvfM5by4Zz24mGBFibEmG-hfn8nRkSJIJ2T8VmpcJ6df1ta=s0-d)
Pois, com o diodo reversamente polarizado não há corrente passando por ele. Isso faz com que o capacitor C1 esteja em série com o indutor L2. Logo, suas correntes devem ser iguais. Como na representação elas estão em sentidos opostos, então uma delas deve ser negativa.
Com a chave aberta temos o diodo conduzindo. Agora quem está em série com o capacitor C1 é o indutor L1. Logo, suas correntes devem ser iguais. Como, na representação, ambas possuem mesmo sentido, então as duas tem o mesmo sinal, ou seja:
![I_{c1}=I_{L1} [;I_{c1}=I_{L1};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_usaDQpyYeQ-JzqsBzoSnG8FgXkjqGBJh84wwSAZFRl2_97_EwYXicSn4M9f8-Bv3B5ELTbIt8eJLKako7DXFfgCpbGVw5aQX6cLUps7eOSDgGRaORqalr46nI=s0-d)
A potência absorvida pela carga é igual a potência fornecida pela fonte, já que estamos considerando todos os componentes como sendo ideais. Assim:
![-V_{o}.I_{L2}=V_E.I_{L1} [;-V_{o}.I_{L2}=V_E.I_{L1};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_s_0HungfnasDMHaQArY9CNLpPHtqgncNYW1bb0a49wBr8d2eycobrH-wLxDLaP45SBlaHjVwS10f6cZf9CwHzHBYK_z5V7lAXA505Gbs9uYgU7JhYpbqjwqGej95QcM-wPdksFVjWOrQ=s0-d)
Manipulando a equação, chegamos a conclusão que:
![\frac{I_{L1}}{I_{L2}}=\frac{-V_o}{V_E} [;\frac{I_{L1}}{I_{L2}}=\frac{-V_o}{V_E};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_sHmHJK3rVQu2AsGl6_rreieAECJj7q4WKR6SFHF7GrMEw4L4WSPkcRglDreHnaki5vPmq2r1ZHsJIXL066htct3L4EC7c0N2jYgsQvUmom7VkEVzdxio8lT_mvIRHXlrl1NlBiuNQ26W9R3waKGiDYaeDMPyqcBFc2ofitrCQ95O8EZmjzAhM=s0-d)
Deixaremos de lado esta equação por enquanto. Agora vamos analisar o fato de que a corrente que passa pelo capacitor em um funcionamento periódico é zero, com isso temos que a corrente que passou pelo capacitor enquanto a chave estava fechada, somada com a corrente que pasou por ele enquanto a chave estava aberta é igual a zero.
Ora, a corrente que passou por ele enquanto a chave estava fechada era![-I_{L2} [;-I_{L2};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_sZuOcH9VNXq3e7TH-LHjr0jAkES94szuRHjB8-NJha03k7xp7-KCi0IMA97XEeD9EZf42tMCjpVfQd9TU6x6n5QZIBWLRSlOeWGnvL6M8jzQ=s0-d) e a corrente que passou por ele enquanto a chave estava aberta era
e a corrente que passou por ele enquanto a chave estava aberta era ![I_{L1} [;I_{L1};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_twwxnY9C68wHs-OjZNdG4mtL5pa00F4IxN2QOvxfgCxthv9193hzdQuWvitA32CPaiZoKeGLcbbAkxr7uhNCx0UL5xqP3qg2bPcjFBz1BC=s0-d) . Dessa forma, temos:
. Dessa forma, temos:
![-I_{L2}DT+I_{L1}(1-D)T=0 [;-I_{L2}DT+I_{L1}(1-D)T=0;]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vmRfy2HfVzGmw92sluWCCXr1Vwmn8lRJoOICWXu-iLKczhhzDG19mfOlpPZcCPr2EKUHWqElWtnU4Wyt3gJ9wxJUAVz6AzGIuyoCHlJ02GwHniWq8IWckXm5_W2IShcQd3oDJn=s0-d)
![I_{L2}DT=I_{L1}(1-D)T [;I_{L2}DT=I_{L1}(1-D)T;]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_srTr4owuEF2JK84dCNsaA7nl3uYBH11XO2sP1dHtwVJu8rADeEQxzV8qPnuUOu5Jy2dhmPm6zi9HQ0Wh-3hKxIPYxUHGKrKxW4bPuT38xp_JBjgqSh-G7EDluYPl_Gyi9rsw=s0-d)
![\frac{I_{L1}}{I_{L2}}=\frac{D}{(1-D)} [;\frac{I_{L1}}{I_{L2}}=\frac{D}{(1-D)};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vf9aCUA3306SiundqwxWS-akZC4Ejlc4wQs_w88quPXCKzR0XejonP4QPEe7Y15rFTdZLSZZsBfOwBIymvCD-04emk_q2rkKXIfY5feHDp1rcls2Lni2Ag69qPqTQXWAjN1ptkZVU7uqVlNO76Bknc8UYBxTF5ZWqy0GoRVTc8AcUeZ0DDnA=s0-d)
Dessa forma, chegamos a conclusão que:
![V_o=-V_E.(\frac{D}{1-D}) [;V_o=-V_E.(\frac{D}{1-D});]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_tHh3XKjhFxB7Whlp5tv-UDs-ctRczQz2I-bgI07N5cxAYsZ-k8cQ783WWpgB7q2qUAajrRV8t6ns-q-VWzO4dO34vfc7n1CVU1dsOjSg6fMq7NgDmKOoYowaelJ_Oa2zHbu_SfSrE-=s0-d)
O sinal de negativo novamente indica que a tensão de saída está invertida com relação a tensão de entrada, que foi o mesmo problema que tivemos com o converosr Buck-Boost.
E com isto terminamos nossa análise do funcionamento em modo contínuo do conversor Cuk. No próximo post analisaremos o conversor SEPIC, que é praticamente o último dos conversores desta sequência de posts. Então, continuem estudando e até a próxima.
Segue abaixo uma imagem do conversor Cuk:
Para analisarmos este conversor, determinaremos, assim como fizemos com os outros, algumas condições que facilitam os cálculos e garantem o funcionamento no modo contínuo e no estado estável.
1. Os valores de indutores são altos e suas correntes são constantes;
2. Os valores dos capacitores são altos e suas tensões constantes;
3. As formas de onda de tensão e corrente são periódicas;
4. A chave (no caso o transistor) fica fechado durante um tempo DT e aberto durante um tempo (1-D)T onde D é a taxa de trabalho e T é o período;
5. Todos os componentes são ideais.
Descobriremos a tensão média no capacitor utilizando a Lei de Kirchhoff na malha externa. Sabendo que durante um período a tensão média nos indutores é zero, calculamos que a tensão média no capacitor durante um período de trabalho é a tensão de entrada menos a tensão de saída, ou seja:
Com a chave fechada, o diodo estará reversamente polarizado. Dessa forma, a corrente no capacitor C1 será:
Pois, com o diodo reversamente polarizado não há corrente passando por ele. Isso faz com que o capacitor C1 esteja em série com o indutor L2. Logo, suas correntes devem ser iguais. Como na representação elas estão em sentidos opostos, então uma delas deve ser negativa.
Com a chave aberta temos o diodo conduzindo. Agora quem está em série com o capacitor C1 é o indutor L1. Logo, suas correntes devem ser iguais. Como, na representação, ambas possuem mesmo sentido, então as duas tem o mesmo sinal, ou seja:
A potência absorvida pela carga é igual a potência fornecida pela fonte, já que estamos considerando todos os componentes como sendo ideais. Assim:
Manipulando a equação, chegamos a conclusão que:
Deixaremos de lado esta equação por enquanto. Agora vamos analisar o fato de que a corrente que passa pelo capacitor em um funcionamento periódico é zero, com isso temos que a corrente que passou pelo capacitor enquanto a chave estava fechada, somada com a corrente que pasou por ele enquanto a chave estava aberta é igual a zero.
Ora, a corrente que passou por ele enquanto a chave estava fechada era
Dessa forma, chegamos a conclusão que:
O sinal de negativo novamente indica que a tensão de saída está invertida com relação a tensão de entrada, que foi o mesmo problema que tivemos com o converosr Buck-Boost.
E com isto terminamos nossa análise do funcionamento em modo contínuo do conversor Cuk. No próximo post analisaremos o conversor SEPIC, que é praticamente o último dos conversores desta sequência de posts. Então, continuem estudando e até a próxima.
terça-feira, 4 de setembro de 2012
Conversor Buck-Boost no modo contínuo
Voltando a série de conversores chaveados, hoje vamos falar do conversor Buck-Boost. Ele tem esse nome pois ele pode tanto rebaixar a tensão (como um conversor Buck) quanto aumentar a tensão (operando como um conversor Boost).
Bom, como sempre, vamos fazer suposições e impor algumas condições, que definem a operação em modo contínuo.
1. Por estar operando no modo contínuo, o indutor sempre estará conduzindo alguma corrente.
2. O circuito está operando no estado estável, ou seja, o transiente do funcionamento já passou.
3. O valor da capacitor é suficientemente grande para manter a tensão na saída constante.
4. A chave fica fechada por um tempo DT e aberta por um tempo (1-D)T.
5. Os componentes são ideais.
Começaremos analisando o circuito com a chave fechada. Nessa situação, temos toda a tensão da fonte sobre o indutor. Também temos o diodo no estado de corte, não permitindo a passagem da corrente da fonte para a carga. A corrente na carga, durante esse tempo, está sendo fornecida pelo capacitor na saída. No indutor, temos que:
![v_{L1}=V_E=L.\frac{di_L}{dt} [;v_{L1}=V_E=L.\frac{di_L}{dt};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_tuM9BxnwLJZpMvQZIErRGB6jMq1S41K_lOgHLsykGy2XSbGLVsJyNDmdgDktKShg8ozPOJxn19wTpWimOQy1drnrvg4zZ5CMhabSkbj5MDtGCX2YkjZPA2zdBsxJ15fB-vjZY04q2nA18bfxXHCVgU=s0-d)
![\frac{di_L}{dt}=\frac{V_E}{L} [;\frac{di_L}{dt}=\frac{V_E}{L};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_sFmcmVu17M2k5Ql9g37EplV7JYXMkLw4KcJRaL0rwcWp7n_ZKGJFf1uQ8UBKh1aFmqynhI5C_7Jj_0MtDCBXibrmRUgUQMiKK8osQhdhZVwhWFAe-0v1gAvST9zGh2eoehEShonGa9i7xkvB7LewqvouUFt5c=s0-d)
Assim vemos que a taxa de variação da corrente no indutor é uma constante. Portanto, a corrente aumenta de forma linear no indutor. Assim, a equação anterior pode ser escrita como:
![\frac{{\Delta}i_L}{{\Delta}t}=\frac{{\Delta}i_L}{DT}=\frac{V_E}{L} [;\frac{{\Delta}i_L}{{\Delta}t}=\frac{{\Delta}i_L}{DT}=\frac{V_E}{L};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_t_DEy5ANNsJ24Osc4O5Vz0XvS6clg-xsACPNdamEYgjmvsAFXxGaIQw3RDDi4e6CFx8U4Krtdb3V_7QrYmuG9iaLZoR1BYwA4gsj4A69d9SssdjVcCAQMdXe86osNNrU3nH5p9RpmTVKyO764FHs6ESWsEmqvGYuoh-gAqjf5lgAwTSybnKK4c4qtCpzLqQhn-Ps1LxjYDZcx2Wj_DfUYH-n-cNCePs1g02i27YVE6rOfazWdqdfIycGU=s0-d)
Assim, a variação da corrente enquanto a chave está fechada é:
![({\Delta}i_L)_{fechada}=\frac{DT.V_E}{L} [;({\Delta}i_L)_{fechada}=\frac{DT.V_E}{L};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_tvng0rr9X53ZF44mlzcEB81xsw0qnRcW2PvgHV5nR58gQMvhDOGZXW7TcqtFRn5ZREaHhMsAJxcEkqlH2IuuBV4F8rV3FOr2n1iPzEwEL3mwO_vWlXvfEtG8gyRsGDkfpF9rd1e7h2lOXhN67LtPVrPJmPjeODQl-_4liWDTiHatw=s0-d)
Passando agora para a análise com a chave aberta. Dessa forma, o diodo passa a ficar diretamente polarizado devido ao indutor, que irá fornecer corrente para a carga e para recarregar o capacitor. Assim podemos ver que o indutor fica em paralelo com a carga (considerando o diodo ideal) e, portanto, tem a mesma tensão que a carga, que é a tensão de saída. Assim, temos:
![v_L=V_S=L.\frac{di_L}{dt} [;v_L=V_S=L.\frac{di_L}{dt};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_tfcDnQTsqUAB3ScnRLFcpXWhNc8mQ4LNuY2FDP8mEmmJXC2le2gXCpBR-1uJCa8pqCwEWNYyifc4Fw3BZ0v2Bs9AupiIn_sq2WR3NMYPMllfaYp_w4M6LVdQl-KVa1Uw95rNGzpRoIh6m9=s0-d)
Utilizando o mesmo raciocínio usado antes, e lembrando que o tempo que a chave fica aberta é (1-D)T, vamos chegar na seguinte expressão:
![({\Delta}i_L)_{aberta}=\frac{V_S(1-D)T}{L} [;({\Delta}i_L)_{aberta}=\frac{V_S(1-D)T}{L};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_t_FVc_6JWgSw41-ZK9thbu_xN2AcxW96BQmylt3Xm4LtMYyteniKrwkYfA9of_p5_c8tt8uxGcwWkVlZFFq22JhYbty14gnDwLJr-jJZvDO5pnVPGh5vskjMe_fQ9VqDUKXN0xYnWYNNG6KXCLjTl83_0IbLlFJ1qwIJEGwLnA9Otj=s0-d)
Porém, na condição 2, dizemos que o circuito estava operando no modo estável. Dessa forma, temos que a corrente no final de um ciclo é exatamente igual a corrente no início de um ciclo. Assim concluímos que a variação de corrente durante um ciclo deve ser zero. Expressando isso matematicamente chegamos em:
![({\Delta}i_L)_{fechada}+({\Delta}i_L)_{aberta}=0 [;({\Delta}i_L)_{fechada}+({\Delta}i_L)_{aberta}=0;]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_tX9VAMEkdFJH6CAGc5OH2CQU517isb5dszpbeM_dmJBbiN7dVgh8BRACH_gLHDNVJckzzRvUC6jDxeivsd3Zyb15q5CyW4IZ3-MGRErm8j6aN6yTvmyPNqQV2lB_lWfmKv1c-36qHzs7ZS6ddBtqAZSaVd06CRSNXyzUQALaTD5zdBt0lDO772gA=s0-d)
![\frac{V_E.DT}{L}+\frac{V_E(1-D)T}{L}=0 [;\frac{V_E.DT}{L}+\frac{V_E(1-D)T}{L}=0;]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vUzEwxjyXvgpWUV1uOVphLilG-TEHm6d0136UMTlCuMp6VbwY-Q54j6Dofu_r6edN0SBq2Boq9KMwU0MRJt8wwB_mZTlU7QnmuC4Q9f0CoB_nUGXxILlE0wIfwUQ54XGt5mrB8HQNYEZy26pXB51rO-f2DXoJVFVXB6eMnx_nm=s0-d)
Enfm, isolando a tensão de saída, temos que:
![V_S=-V_E(\frac{D}{1-D}) [;V_S=-V_E(\frac{D}{1-D});]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vmmQNYrYs_L2VvJZmxBJ7fV4rzRCT17e3_iWaP4f6Wrkp3LHtLUudatqXzX7AD2Kzk3W4eLrF0OxNXYQpRTO2t4N6NfdcGwaerDknL3o7rYuVgfqR69q_DDVjpPP6ts-qtSXUNAY8=s0-d)
Agora, vamos analisar os dados de nossa dedução. O módulo da tensão na saída pode ser maior ou menor que a tensão de entrada, sendo exatamente igual se fizermos D=0.5. Também percebemos aquele sinal de negativo na expressão da tensão de saída. Isso se deve ao fato de a tensão na saída deste conversor estar invertida em relação a tensão de entrada. Isso é, em geral, uma desvantagem, que não existe nos outros conversores que estudamos. Observando nossa análise, percebemos que a tensão de entrada nunca está eletricamente conectada com a carga. A energia é primeiro armazenada no indutor para, somente depois, ser transferida à carga. Por isso alguma vezes o conversor Buck-Boost é conhecido como conversor indireto.
Vamos fazer um pouco mais de análise "secundária" para descobrir outras coisas sobre este circuito:
A potência de saída é:
![P_S=\frac{V_S^2}{R} [;P_S=\frac{V_S^2}{R};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vke850ugKU1giNlHjua4ukhsjoefuEhcBVHDYfHWsdtOYnAXvwMEcYkJxqVy9JtjFg-YLbseKERG4QfnEzoHlJzTwyvhDC_XDd-ldYYMg6e55opz82aQXTuXKYF6q75pw1Y0Pq=s0-d)
A potência de entrada é dada por:
![P_E=V_E.I_E [;P_E=V_E.I_E;]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_uzI5sQJXljs_0jFINLY22NhnVMGZPxrz_hvuP7ACWCqFolQJaAx_TZxBdqZFo8cWd9o66ipldtamYjyVD9Jg4FOhyUzhY6CGbQKNsonGru=s0-d)
Sendo todos os componentes ideais, toda a energia na entrada é transferida para a saída. Portanto, a potência da entrada é igual a da saída.
![\frac{V_S^2}{R}=V_E.I_E [;\frac{V_S^2}{R}=V_E.I_E;]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_uFktRB6UxXDW9ae4TKlM6QlG61symLhbI-WgVvmiIvzaWG3ot7ZqfcFwP6Ow5kMQ-RRh1uWOnLOjgdm2b7hKz8aVA-FUr6GjKXQAJdCKLh3pKl5fRU2s6Ytzki8ObktMam141tFC9quA=s0-d)
Mas, a corrente média na fonte, ou seja, na entrada, pode ser relacionada com a corrente no indutor por:
![I_E=I_L.D [;I_E=I_L.D;]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_u739xvFAWBr8FvsFsn5kvmVSAix9T4_yyfScFsR2hUQDglVoTW77pgPuCY6dOLHUo8gAN6xJWeJjMNF-PN60595YfcjWuQ2ZaenK9TuPE=s0-d)
Substituindo na outra equação, temos:
![\frac{V_S^2}{R}=V_E.I_L.D [;\frac{V_S^2}{R}=V_E.I_L.D;]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vk3ETpZ-xY2uyX4uAg1TS4HCbSZL2vSzXzgGFOGOM0lpfe6selBktcwZyyE7wgruSn26WIDrYdmZJ0_560k4HTjuqek6JuywZOv51IHJ-_fMX7KYYh25ouVTCssqBhwc4mWSUv0Q19Lre2=s0-d)
Mas, lembrando da equação que deduzimos para a tensão de saída, e substituindo seu resultado aqui, obtemos:
![I_L=\frac{V_E.D}{R(1-D)^2} [;I_L=\frac{V_E.D}{R(1-D)^2};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vtb3xgV_iRJxyRjWjJNOdyA6uRpYs8E-DG2EJ__pku18FxjnHdUVZzb9otJVYFql-2rWrOIbGKT4Alm9zpSvm__tM2aVhVAUtC5OCbfaMldN1EETca5bFHHMZUAlyJn2pGX8Nztu_DVGab7g=s0-d)
As correntes máximas e mínimas no indutor são determinadas somando a corrente média à metada da variação da corrente. Assim temos:
![I_{MAX}=I_L+\frac{{\Delta}i_L}{2}=\frac{V_E.D}{R(1-D)^2}+\frac{V_E.DT}{2L} [;I_{MAX}=I_L+\frac{{\Delta}i_L}{2}=\frac{V_E.D}{R(1-D)^2}+\frac{V_E.DT}{2L};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_u6BtdjqHQW3Vob8uwR36Jyva5KNWj9QZ6mADu4YOqR9ZQKkt4dp3T2LFbTdq1s59osk3g1oa7MLweAwqBMruOC5Fp-stqRFxxpXDP_PwE37NEtY2_U-XW5Bo84Dfd1uNqd8ofesj-x__ofiflEkSzdosFgjgcAVNFcOSA-sezdBzE0E42b-zk5cxR-0eM9jhNWdznhM-rjdBo-KE-VSxM9aAZDovHRRURy_pgQm5Hcqne6oLxIt1eaKr1h4A=s0-d)
![I_{MIN}=I_L-\frac{{\Delta}i_L}{2}=\frac{V_E.D}{R(1-D)^2}-\frac{V_E.DT}{2L} [;I_{MIN}=I_L-\frac{{\Delta}i_L}{2}=\frac{V_E.D}{R(1-D)^2}-\frac{V_E.DT}{2L};]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_scAB86s9wcfthgQUPvlG_ygUN7eet5aDluMHR0wKqMCjdnQrBWTVZZUUqIO81Dn7yc-56mGhNOLtdct4CeEYxy4lV70cktxjM6K29xc0T3bLLhx2NOBi2eeeFxKFsijnG7qvlTtEdS8jwBb3Pq_gn6BAytFh8g0-1i-DI-zBWubx80vrh5cHsyOG_e7fdQeeIq0F7CpssK3Kv-lWqA0zcbo6cn-gRnlnZiQC1JSeyklgfuKGoXBh0UWwbOyw=s0-d)
Assim, temos muitos dados que definem o funcionamento do conversor Buck-Boost. Claro que para projetar um destes é preciso se ater aos detalhes, mas o foco desta série é, neste primeiro momento, obter o entendimento do funcionamento destes conversores.
E por hoje era isso, então se cuidem e continuem estudando. Até o próximo post da série de conversores chaveados, que sairá em breve. Abraço. Fui...
Bom, como sempre, vamos fazer suposições e impor algumas condições, que definem a operação em modo contínuo.
1. Por estar operando no modo contínuo, o indutor sempre estará conduzindo alguma corrente.
2. O circuito está operando no estado estável, ou seja, o transiente do funcionamento já passou.
3. O valor da capacitor é suficientemente grande para manter a tensão na saída constante.
4. A chave fica fechada por um tempo DT e aberta por um tempo (1-D)T.
5. Os componentes são ideais.
Começaremos analisando o circuito com a chave fechada. Nessa situação, temos toda a tensão da fonte sobre o indutor. Também temos o diodo no estado de corte, não permitindo a passagem da corrente da fonte para a carga. A corrente na carga, durante esse tempo, está sendo fornecida pelo capacitor na saída. No indutor, temos que:
Assim vemos que a taxa de variação da corrente no indutor é uma constante. Portanto, a corrente aumenta de forma linear no indutor. Assim, a equação anterior pode ser escrita como:
Assim, a variação da corrente enquanto a chave está fechada é:
Passando agora para a análise com a chave aberta. Dessa forma, o diodo passa a ficar diretamente polarizado devido ao indutor, que irá fornecer corrente para a carga e para recarregar o capacitor. Assim podemos ver que o indutor fica em paralelo com a carga (considerando o diodo ideal) e, portanto, tem a mesma tensão que a carga, que é a tensão de saída. Assim, temos:
Utilizando o mesmo raciocínio usado antes, e lembrando que o tempo que a chave fica aberta é (1-D)T, vamos chegar na seguinte expressão:
Porém, na condição 2, dizemos que o circuito estava operando no modo estável. Dessa forma, temos que a corrente no final de um ciclo é exatamente igual a corrente no início de um ciclo. Assim concluímos que a variação de corrente durante um ciclo deve ser zero. Expressando isso matematicamente chegamos em:
Enfm, isolando a tensão de saída, temos que:
Agora, vamos analisar os dados de nossa dedução. O módulo da tensão na saída pode ser maior ou menor que a tensão de entrada, sendo exatamente igual se fizermos D=0.5. Também percebemos aquele sinal de negativo na expressão da tensão de saída. Isso se deve ao fato de a tensão na saída deste conversor estar invertida em relação a tensão de entrada. Isso é, em geral, uma desvantagem, que não existe nos outros conversores que estudamos. Observando nossa análise, percebemos que a tensão de entrada nunca está eletricamente conectada com a carga. A energia é primeiro armazenada no indutor para, somente depois, ser transferida à carga. Por isso alguma vezes o conversor Buck-Boost é conhecido como conversor indireto.
Vamos fazer um pouco mais de análise "secundária" para descobrir outras coisas sobre este circuito:
A potência de saída é:
A potência de entrada é dada por:
Sendo todos os componentes ideais, toda a energia na entrada é transferida para a saída. Portanto, a potência da entrada é igual a da saída.
Mas, a corrente média na fonte, ou seja, na entrada, pode ser relacionada com a corrente no indutor por:
Substituindo na outra equação, temos:
Mas, lembrando da equação que deduzimos para a tensão de saída, e substituindo seu resultado aqui, obtemos:
As correntes máximas e mínimas no indutor são determinadas somando a corrente média à metada da variação da corrente. Assim temos:
Assim, temos muitos dados que definem o funcionamento do conversor Buck-Boost. Claro que para projetar um destes é preciso se ater aos detalhes, mas o foco desta série é, neste primeiro momento, obter o entendimento do funcionamento destes conversores.
E por hoje era isso, então se cuidem e continuem estudando. Até o próximo post da série de conversores chaveados, que sairá em breve. Abraço. Fui...
Assinar:
Comentários (Atom)