Conversor Cuk no Modo Contínuo

Olá a todos, hoje falaremos de uma topologia de conversor chaveado CC-CC chamada Conversor Cuk. Ele serve para elevar ou rebaixar a tensão de entrada e, assim como o conversor Buck-Boost, e também possui a polaridade de saída invertida com relação a entrada. Sua principal diferença é o fato de que esta topologia usa um capacitor para fazer a transferência de energia entre os dois estágios, diferente do conversor Buck-Boost que utiliza um indutor.

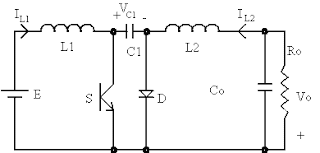
Segue abaixo uma imagem do conversor Cuk:

Para analisarmos este conversor, determinaremos, assim como fizemos com os outros, algumas condições que facilitam os cálculos e garantem o funcionamento no modo contínuo e no estado estável.

1. Os valores de indutores são altos e suas correntes são constantes;
2. Os valores dos capacitores são altos e suas tensões constantes;
3. As formas de onda de tensão e corrente são periódicas;
4. A chave (no caso o transistor) fica fechado durante um tempo DT e aberto durante um tempo (1-D)T onde D é a taxa de trabalho e T é o período;
5. Todos os componentes são ideais.

Descobriremos a tensão média no capacitor utilizando a Lei de Kirchhoff na malha externa. Sabendo que durante um período a tensão média nos indutores é zero, calculamos que a tensão média no capacitor durante um período de trabalho é a tensão de entrada menos a tensão de saída, ou seja:



Com a chave fechada, o diodo estará reversamente polarizado. Dessa forma, a corrente no capacitor C1 será:




Pois, com o diodo reversamente polarizado não há corrente passando por ele. Isso faz com que o capacitor C1 esteja em série com o indutor L2. Logo, suas correntes devem ser iguais. Como na representação elas estão em sentidos opostos, então uma delas deve ser negativa.

Com a chave aberta temos o diodo conduzindo. Agora quem está em série com o capacitor C1 é o indutor L1. Logo, suas correntes devem ser iguais. Como, na representação, ambas possuem mesmo sentido, então as duas tem o mesmo sinal, ou seja:



A potência absorvida pela carga é igual a potência fornecida pela fonte, já que estamos considerando todos os componentes como sendo ideais. Assim:



Manipulando a equação, chegamos a conclusão que:



Deixaremos de lado esta equação por enquanto. Agora vamos analisar o fato de que a corrente que passa pelo capacitor em um funcionamento periódico é zero, com isso temos que a corrente que passou pelo capacitor enquanto a chave estava fechada, somada com a corrente que pasou por ele enquanto a chave estava aberta é igual a zero.

Ora, a corrente que passou por ele enquanto a chave estava fechada era e a corrente que passou por ele enquanto a chave estava aberta era . Dessa forma, temos:







Dessa forma, chegamos a conclusão que:



O sinal de negativo novamente indica que a tensão de saída está invertida com relação a tensão de entrada, que foi o mesmo problema que tivemos com o converosr Buck-Boost.

E com isto terminamos nossa análise do funcionamento em modo contínuo do conversor Cuk. No próximo post analisaremos o conversor SEPIC, que é praticamente o último dos conversores desta sequência de posts. Então, continuem estudando e até a próxima.

Conversor Buck-Boost no modo contínuo

Voltando a série de conversores chaveados, hoje vamos falar do conversor Buck-Boost. Ele tem esse nome pois ele pode tanto rebaixar a tensão (como um conversor Buck) quanto aumentar a tensão (operando como um conversor Boost).

Bom, como sempre, vamos fazer suposições e impor algumas condições, que definem a operação em modo contínuo.

1. Por estar operando no modo contínuo, o indutor sempre estará conduzindo alguma corrente.
2. O circuito está operando no estado estável, ou seja, o transiente do funcionamento já passou.
3. O valor da capacitor é suficientemente grande para manter a tensão na saída constante.
4. A chave fica fechada por um tempo DT e aberta por um tempo (1-D)T.
5. Os componentes são ideais.

Começaremos analisando o circuito com a chave fechada. Nessa situação, temos toda a tensão da fonte sobre o indutor. Também temos o diodo no estado de corte, não permitindo a passagem da corrente da fonte para a carga. A corrente na carga, durante esse tempo, está sendo fornecida pelo capacitor na saída. No indutor, temos que:





Assim vemos que a taxa de variação da corrente no indutor é uma constante. Portanto, a corrente aumenta de forma linear  no indutor. Assim, a equação anterior pode ser escrita como:



Assim, a variação da corrente enquanto a chave está fechada é:



Passando agora para a análise com a chave aberta. Dessa forma, o diodo passa a ficar diretamente polarizado devido ao indutor, que irá fornecer corrente para a carga e para recarregar o capacitor. Assim podemos ver que o indutor fica em paralelo com a carga (considerando o diodo ideal) e, portanto, tem a mesma tensão que a carga, que é a tensão de saída. Assim, temos:



Utilizando o mesmo raciocínio usado antes, e lembrando que o tempo que a chave fica aberta é (1-D)T, vamos chegar na seguinte expressão:



Porém, na condição 2, dizemos que o circuito estava operando no modo estável. Dessa forma, temos que a corrente no final de um ciclo é exatamente igual a corrente no início de um ciclo. Assim concluímos que a variação de corrente durante um ciclo deve ser zero. Expressando isso matematicamente chegamos em:





Enfm, isolando a tensão de saída, temos que:



Agora, vamos analisar os dados de nossa dedução. O módulo da tensão na saída pode ser maior ou menor que a tensão de entrada, sendo exatamente igual se fizermos D=0.5. Também percebemos aquele sinal de negativo na expressão da tensão de saída. Isso se deve ao fato de a tensão na saída deste conversor estar invertida em relação a tensão de entrada. Isso é, em geral, uma desvantagem, que não existe nos outros conversores que estudamos. Observando nossa análise, percebemos que a tensão de entrada nunca está eletricamente conectada com a carga. A energia é primeiro armazenada no indutor para, somente depois, ser transferida à carga. Por isso alguma vezes o conversor Buck-Boost é conhecido como conversor indireto.

Vamos fazer um pouco mais de análise "secundária" para descobrir outras coisas sobre este circuito:

A potência de saída é:



A potência de entrada é dada por:



Sendo todos os componentes ideais, toda a energia na entrada é transferida para a saída. Portanto, a potência da entrada é igual a da saída.



Mas, a corrente média na fonte, ou seja, na entrada, pode ser relacionada com a corrente no indutor por:



Substituindo na outra equação, temos:



Mas, lembrando da equação que deduzimos para a tensão de saída, e substituindo seu resultado aqui, obtemos:



As correntes máximas e mínimas no indutor são determinadas somando a corrente média à metada da variação da corrente. Assim temos:






Assim, temos muitos dados que definem o funcionamento do conversor Buck-Boost. Claro que para projetar um destes é preciso se ater aos detalhes, mas o foco desta série é, neste primeiro momento, obter o entendimento do funcionamento destes conversores.

E por hoje era isso, então se cuidem e continuem estudando. Até o próximo post da série de conversores chaveados, que sairá em breve. Abraço. Fui...