Lógica Combinacional - Portas Lógicas

Olá a todos. Hoje vamos começar a falar sobre eletrônica digital e, para introduzir esse novo tema, vamos falar um pouco de lógica combinacional. O que ela é, para que ela serve e o que são portas lógicas.

Antes de começarmos acho interessante esclarecer algo que era uma dúvida minha antes de estudar eletrônica digital. Nós falaremos muito sobre 1's e 0's, mas, o que eles são? A explicação comum é simples: 1 significa que tem tensão e 0 que não tem. Porém eu não acho essa explicação muito esclarecedora, então quero dissertar um pouco sobre isso.

Existem diversas famílias de portas lógicas, que são os constituintes fundamentais dos circuitos digitais. Comumente se trabalha com apenas duas: TTL e CMOS. As portas lógicas da família TTL (que significa Transistor-Transistor Logic) são feitos de transistores bipolares ou FET's e são alimentados com 5V. Idealmente 5V equivalem a 1 e 0V equivalem a 0. Mas na realidade existem faixas de tensão que correspondem a esses níveis lógicos. Entre 0 e 0,8V é nível lógico 0. Entre 2,4 e 5V é nível lógico 1. Entre os valores de 0,8 até 2,4V temos um nível lógico indeterminado, que os circuitos podem entender tanto como 0 quanto como 1. Como é impossível prever o que irá acontecer nessa situação, tais níveis de tensão não são desejados dentro dos circuitos digitais.

Já na outra família que comentei, CMOS (Complementary Metal Oxide Semiconductor, se não me engano) é construída usando a tecnologia de transistores MOSFET complementares. Eles são alimentados com 5V também e sua faixa de nível 0 é entre 0 e 1,5V, e sua faixa de nível 1 é entre 3,5 e 5V. A faixa entre 1,5 e 3,5V constitui nível indeterminado e também deve ser evitado. Mais adiante eu farei um post somente sobre famílias lógicas, comentando todos os detalhes. Agora já podemos falar sobre Lógica Combinacional.

Lógica Combinacional é um tipo de lógica digital. Quando um circuito digital é combinacional, o estado lógico da saída depende exclusivamente do estado atual das entradas. Os circuitos digitais respeitam uma tabela verdade, que é uma tabela que nos informa os estados de saída para todas as combinações lógicas das entradas. Um exemplo disso pode ser visto na figura abaixo.

O número de possibilidades é dado por 2 elevado na "n", onde n é o número de entradas. Como temos duas entradas (A e B), temos então 4 possibilidades. A tabela verdade acima mostra o estado da saída para  qualquer uma das 4 combinações de entrada. Por exemplo, se o nível lógico de A for igual a 0 e o nível lógico de B for igual a 1, a saída, naquele instante, assumirá o nível lógico 1.

Claro que essa é uma tabela de exemplo, que é extremamente simples, mas os circuitos combinacionais podem criar qualquer tabela verdade, de complexidade cada vez maior. Para montarmos tais circuitos combinacionais, nós temos os "tijolinhos" da eletrônica digital, que se chamam portas lógicas. Essas portas lógicas executam operações lógicas que podem ser representadas por uma tabela verdade, e a combinação dessas portas lógicas em um circuito nos permitem fazer qualquer operação e, portanto, qualquer tabela verdade. Então, vamos conhecer essas portas lógicas:

Vamos começar pela primeira porta, letra (a), que é a porta NOT (Inversora). Essa porta inverte o nível da entrada. Como podemos ver pela tabela verdade, se A for 0 a saída é 1 e, se A for 1, a saída é 0.

Vamos agora para a última porta, letra (e), que é a porta OR (OU). Sua lógica é a seguinte: Se uma entrada for 1, OU a outra entrada for 1, OU as duas entradas forem 1, a saída será 1. Essa porta só terá a saída em 0 se ambas as entradas forem zero. Esse raciocínio se aplica para portas OU com mais de duas entradas. Essas portas também só terão 0 na saída se todas as entradas (seja quantas forem) estiverem com nível lógico 0.

Passando agora para a penúltima porta, letra (d), que é a porta AND (E). Sua lógica é a seguinte: A saída só assumirá nível lógico 1 se uma entrada tiver 1 E a outra entrada tiver 1 também. Se pelo menos uma das entradas possuir nível 0, a saída também será 0. Mesma lógica se aplica a portas E com mais entradas, onde a saída só será 1 se todas as entradas (seja quantas forem) apresentarem nível 1.

Vamos para a terceira porta, letra (c), que é a porta NOR (OU Invertida). Ela não passa de uma porta OU cuja saída é jogada em uma inversora, que é representado pela pequena bolinha na saída da porta. Se você comparar esta tabela com a tabela da porta OU normal, você perceberá que, se em uma situação a OR normal tem 0 na saída, a NOR tem 1 e vice-versa. A lógica dessa porta então é a seguinte: Se uma entrada tiver 1 OU a outra entrada tiver 1 OU as duas entradas possuírem 1, a saída será 0. Somente se todas as entradas forem 0 a saída assumirá o nível 1.

Vamos enfim para a segunda porta, letra (b), que é a porta NAND (E Invertida). Ela também não passa de uma porta AND simples cuja saída é jogada em uma inversora, o que pode ser visto pela pequena bolinha na saída, conhecida como bolha de inversão. Novamente, se compararmos esta tabela com a E simples, veremos que para qualquer situação que a AND simples apresente 1 na saída, a NAND irá ter 0 na saída, e vice-versa. Sua lógica é a seguinte: Se em uma entrada eu tenho 1 E na outra entrada também tenho 1, minha saída será 0. Nas outras situações possíveis, minha saída será 1. 

Esses dois carinhas não são portas lógicas propriamente ditas, mas vamos tratá-las como tal. A primeira se chama XOR, abreviação de Exclusive OR (OU Exclusiva). Sua lógica é semelhante a da porta OR. Ela apresenta 1 na saída se tiver 1 em uma entrada OU 1 na outra. Porém, se ambas as entradas forem 1, a saída será 0 (diferindo da porta OR nesse aspecto).

A segunda porta é a XNOR, abreviação de Exclusive NOR (OU Invertida Exclusiva). Ela basicamente funciona como a porta XOR com uma Inversora na saída. Sua lógica é a seguinte: A saída será 1 se ambas as entradas possuírem 1 ou ambas possuírem 0. Caso as entradas difiram entre si, sua saída será 0.

E essas são as portas lógicas, que executam operações lógicas simples e que, quando combinadas, podem fazer circuitos complexos e bastante interessantes. Gostaria de ressaltar algo: as portas NAND e NOR são portas "universais". Isso pois podemos "fazer" qualquer porta com elas, ou seja, realizar qualquer operação lógica usando somente essas portas. Por exemplo, podemos fazer uma inversora com a NAND ou com a NOR, da seguinte maneira:

Fazendo a mesma informação entrar por ambas as entradas de uma NAND, fazemos uma inversora com ela. Assim, se entrar 1 sairá 0 e, ao entrar 0 sairá 1. Procedendo da mesma forma, também podemos transformar a porta NOR em uma inversora. Se você verificar a tabela verdade dessa portas e olhar somente as situações onde ambas as entradas são iguais, verá que elas se comportam como inversoras.

A tabela acima mostra como montar outras portas a partir a NOR e NAND. A figura da letra "a" mostra como montar as inversoras, como já comentamos. As figuras "b" nos mostram como executar a lógica AND (E) somente com portas NAND e somente com portas NOR. A figura da letra "c" nos mostra como executar a lógica OR (OU) somente com portas NAND e, depois, somente com portas NOR.

A figura acima mostra como podemos montar uma porta XOR somente com portas NOR. Se colocarmos um inversor na saída (e vimos que isto também pode ser feito somente com portas NOR) nós passaremos a ter a porta XNOR, também implementada somente com NOR.

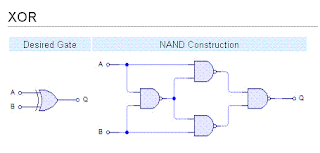
E dessa forma implementamos a porta XOR somente com portas NAND. Para obtermos a XNOR, basta que coloquemos uma inversora na saída, que também pode ser feita somente com portas NAND. Como vimos, podemos implementar qualquer porta usando somente as portas NAND e NOR. É devido a isso que elas são chamadas de portas universais.

Uma curiosidade: somente o conteúdo deste post foi suficiente para levar o homem a Lua. Eu digo isso pois o sistema de computação da nave Apollo foi feita usando somente portas lógicas e, se não me engano, foi todo feito usando somente portas NOR. Porém não tenho certeza disso. O que eu tenho certeza é que existe um livro chamado "Digital Apollo" que conta a história da eletrônica da nave e que é muito bom, porém eu acho que só tem em inglês. Enfim, vale à pena fazer um esforço pra ler.

Por hoje era isso. Nos próximos posts sobre eletrônica digital eu quero mostrar exemplos de circuitos lógicos combinacionais, falar sobre o sistema de numeração binário e a Álgebra de Boole, que é a matemática por trás das operações lógicas executadas pelas portas que vimos hoje. Isso irá contextualizar o conteúdo deste post e fará você entender, por exemplo, por que podemos montar qualquer porta usando somente NAND e NOR. Mas isso fica para uma próxima aventura... Enquanto isso se cuidem e continuem estudando. Abraço!